Flip-flop circuits
4 stars based on
54 reviews
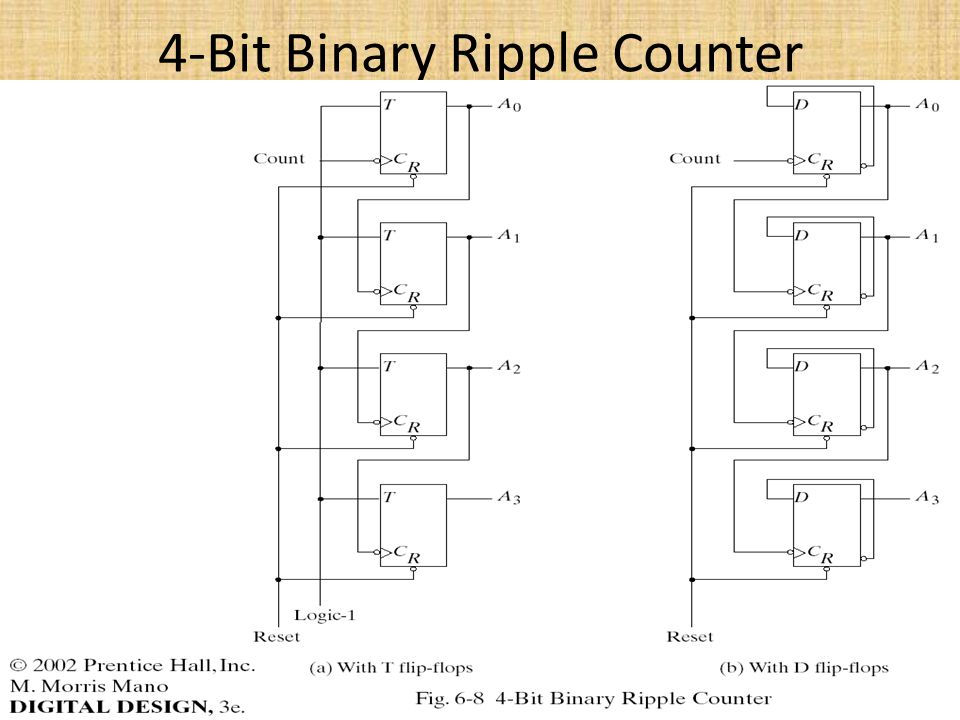
In our initial discussion on counters A Basic Digital Counterwe noted the need to have all flip-flops in a counter to operate in unison with each other, so that all bits in the ouput count would change 4 bit ripple counter using t flipflop truth tables at the same time.
To accomplish this, we need to apply the same clock pulse to all flip-flops. However, we do not want all flip-flops to change state with every clock pulse. Therefore, we'll need to add some controlling gates to determine when each flip-flop is allowed to change state, and when it is not. This requirement denies us the use of T flip-flops, but does require that we still use edge-triggered circuits. To determine the gates required at each flip-flop input, let's start by drawing up a truth table for all states of the counter.
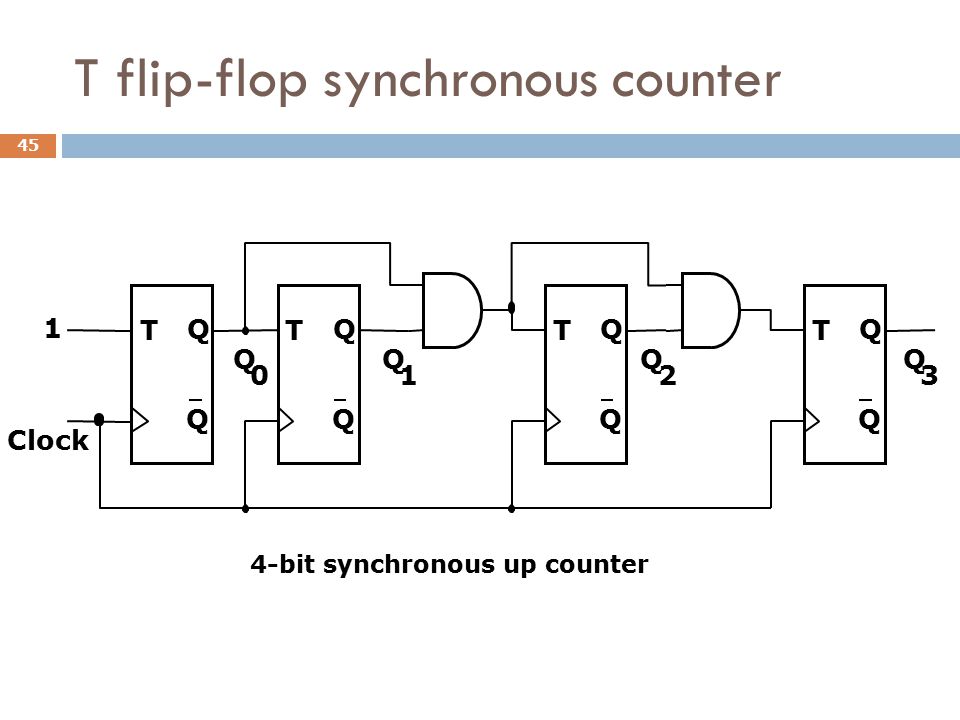
Such a table is shown 4 bit ripple counter using t flipflop truth tables the right. Looking first at output A, we note that it must change state with every input clock pulse. Therefore, we could use a T flip-flop here if we wanted to. We won't do so, just to make all of our flip-flops the same.
But even with JK flip-flops, all we need to do here is to connect both the J and K inputs of this flip-flop to logic 1 in order to get the correct activity. Flip-flop B is a bit more complicated. This output must change state only on every other input clock pulse. Looking at the truth table again, output B must be ready to change states whenever output A is a logic 1, but not when A is a logic 0. 4 bit ripple counter using t flipflop truth tables we recall the behavior of the JK flip-flopwe can see that if we connect output A to the J and K inputs of flip-flop B, we will see output B behaving correctly.
Continuing this line of reasoning, output C may change state only when both A and B are logic 1. Therefore we will need a two-input AND gate at the inputs to flip-flop C.
When we started our look into counters, we noted a lot of applications involving numeric displays: These applications require a decimal count in most cases, and a count from 0 to 5 for some digits in a clock display.
Can we use a method of gating, such as we used above in the synchronous binary counter, to shorten the counting sequence to the appropriate extent? Obviously there is a way, since digital clocks and watches do exist and do work. Starting on the next page, we'll see how.