4 bit ripple carry adder subtractor verilog code

Adder/Subtractor

4 stars based on 58 reviews

In this project, we will design arithmetic circuits using an FPGA. We will build a 4-bit magnitude comparator, a ripple-carry adder, and a multiplier circuit. You can challenge yourself by integrating all of those circuits together with some multiplexers to build an arithmetic logic unit ALU. A magnitude comparator is a device that receives two N-bit inputs and asserts one of three possible outputs depending on whether one input is greater than, less than, or equal to the other simpler comparators, called equality comparators, provide a single output that is asserted whenever the two inputs are equal.

The truth table of a bit-sliced magnitude comparator and the 4 bit ripple carry adder subtractor verilog code diagram of a magnitude comparator are shown in Figs. Adder circuits add two N-bit operands to produce an N-bit result and a carry out signal the carry out is a '1' only when the addition result requires more than N-bits.

The logic graph in Fig. The highlighted bit pairs and the associated carries show that a bit-slice adder circuit must process three inputs the two addend bits and a carry-in from the previous stage and produce two outputs the sum bit and a carry out bit.

It is possible to capitalize on this observation, and create a smaller bit-slice circuit for use in the LSB position that does not have a carry-in input.

The ripple carry adder block diagram is displayed in Fig. Hardware multipliers, based directly on adder architectures, have become indispensable in modern computers. In this algorithm, one partial product is created for each bit in the multiplier—the first partial product is created by the LSB of the multiplier, the second partial product is created by the second bit in the multiplier, and so forth.

The partial product bits need to be fed to an array of full adders and half adders where appropriatewith 4 bit ripple carry adder subtractor verilog code adders shifted to the left as indicated by the multiplication example.

The final partial products are added with a CLA circuit. Note that some full-adder circuits bring signal values into the carry-in inputs instead of carry's from the neighboring stage. This is a valid use of the full-adder circuit; the full adder simply adds any three bits applied to its inputs.

The circuit for a partial product and the block diagram of the multiplier is shown in Fig. Up to this point, you are expected to be able to describe circuits structurally. Based on the block diagram shown above in Fig. Before deploying your circuit on your board, write a test bench to verify that your circuit is correct.

Unlike the adder and subtractor, multipliers do not have an operator support in Verilog, mostly due to the fact that there are various ways to implement a multiplier which trade off power, hardware resource, and speed.

So implementing a multiplier structurally is the only solution. Back 4 bit ripple carry adder subtractor verilog code the list Share: Design Arithmetic Circuits Project 4 bit ripple carry adder subtractor verilog code Before you begin, you should: Have your FPGA board set up. Be able to describe digital circuits using logic operators. Be able to write test bench and simulate circuit using ISim. After you're done, you should: Understand how magnitude comparators, ripple-carry adders, and multipliers work.

Be 4 bit ripple carry adder subtractor verilog code to describe magnitude comparators, ripple-carry adders, and multipliers structurally. Design a 4-bit Comparator Create a Verilog module for a bit-sliced magnitude comparator according to the truth table presented in Fig. Design a 4-bit Binary Adder Create a Verilog module for a full adder. Design a 4-bit Multiplier Up to this point, you are expected to be able to describe circuits structurally.

Now that you've completed this project, try these modifications: Implement a 4-bit borrow ripple subtractor using bit-sliced design methodology and describe it structurally in Verilog. Inputs and Output of the ALU are 4-bit binary numbers in 2's complement. Other product and company names mentioned herein are trademarks or trade names of their respective companies.

Bitcoin mining ph strips

Como nao trocar bitcoinerros fatais compartilhados
Paysafecard bitcoin tauschen state

Unity3d bitcoin mining

Atlanta global advisors bitcoin

Coingecko bitcoin exchange rate
Can i buy bitcoin with paypal on bitstamp
Wymiana dogecoin na bitcoin news

21 bitcoin computer hash rate test

42 comments

Kryptonics route 62 wheels review

An adder is a digital circuit that performs addition of numbers. In many computers and other kinds of processors adders are used in the arithmetic logic units or ALU. They are also utilized in other parts of the processor, where they are used to calculate addresses , table indices, increment and decrement operators , and similar operations. Although adders can be constructed for many number representations , such as binary-coded decimal or excess-3 , the most common adders operate on binary numbers.

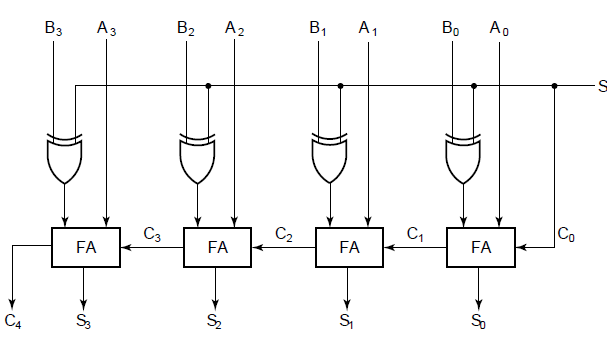
In cases where two's complement or ones' complement is being used to represent negative numbers , it is trivial to modify an adder into an adder—subtractor. Other signed number representations require more logic around the basic adder. The half adder adds two single binary digits A and B. It has two outputs, sum S and carry C. The carry signal represents an overflow into the next digit of a multi-digit addition. With the addition of an OR gate to combine their carry outputs, two half adders can be combined to make a full adder.

The input variables of a half adder are called the augend and addend bits. The output variables are the sum and carry. The truth table for the half adder is:. A full adder adds binary numbers and accounts for values carried in as well as out.

A one-bit full-adder adds three one-bit numbers, often written as A , B , and C in ; A and B are the operands, and C in is a bit carried in from the previous less-significant stage. The circuit produces a two-bit output. A full adder can be implemented in many different ways such as with a custom transistor -level circuit or composed of other gates. In this implementation, the final OR gate before the carry-out output may be replaced by an XOR gate without altering the resulting logic.

Using only two types of gates is convenient if the circuit is being implemented using simple IC chips which contain only one gate type per chip. Assumed that an XOR-gate takes 1 delays to complete, the delay imposed by the critical path of a full adder is equal to. It is possible to create a logical circuit using multiple full adders to add N -bit numbers.

Each full adder inputs a C in , which is the C out of the previous adder. This kind of adder is called a ripple-carry adder RCA , since each carry bit "ripples" to the next full adder. The layout of a ripple-carry adder is simple, which allows fast design time; however, the ripple-carry adder is relatively slow, since each full adder must wait for the carry bit to be calculated from the previous full adder.

The gate delay can easily be calculated by inspection of the full adder circuit. Each full adder requires three levels of logic. The carry-in must travel through n XOR-gates in adders and n carry-generator blocks to have an effect on the carry-out. To reduce the computation time, engineers devised faster ways to add two binary numbers by using carry-lookahead adders CLA.

They work by creating two signals P and G for each bit position, based on whether a carry is propagated through from a less significant bit position at least one input is a 1 , generated in that bit position both inputs are 1 , or killed in that bit position both inputs are 0. In most cases, P is simply the sum output of a half adder and G is the carry output of the same adder. After P and G are generated, the carries for every bit position are created.

Some other multi-bit adder architectures break the adder into blocks. It is possible to vary the length of these blocks based on the propagation delay of the circuits to optimize computation time.

These block based adders include the carry-skip or carry-bypass adder which will determine P and G values for each block rather than each bit, and the carry select adder which pre-generates the sum and carry values for either possible carry input 0 or 1 to the block, using multiplexers to select the appropriate result when the carry bit is known.

By combining multiple carry-lookahead adders, even larger adders can be created. This can be used at multiple levels to make even larger adders. Other adder designs include the carry-select adder , conditional sum adder , carry-skip adder , and carry-complete adder. If an adding circuit is to compute the sum of three or more numbers, it can be advantageous to not propagate the carry result.

Instead, three-input adders are used, generating two results: The sum and the carry may be fed into two inputs of the subsequent 3-number adder without having to wait for propagation of a carry signal. After all stages of addition, however, a conventional adder such as the ripple-carry or the lookahead must be used to combine the final sum and carry results. A full adder can be viewed as a 3: The carry-out represents bit one of the result, while the sum represents bit zero.

Likewise, a half adder can be used as a 2: Such compressors can be used to speed up the summation of three or more addends. If the addends are exactly three, the layout is known as the carry-save adder. If the addends are four or more, more than one layer of compressors is necessary, and there are various possible design for the circuit: This kind of circuit is most notably used in multipliers, which is why these circuits are also known as Dadda and Wallace multipliers. From Wikipedia, the free encyclopedia.

Digital Logic and Computer Design. Written at Heverlee, Belgium. Retrieved from " https: Computer arithmetic Adders electronics Binary logic. Views Read Edit View history. In other projects Wikimedia Commons. This page was last edited on 12 May , at By using this site, you agree to the Terms of Use and Privacy Policy.

tfc-salamander.com